大衍求一术（dayanqiuyishu）
南宋数学家秦九韶提出的解一次同余式组的方式。此法可远溯到公元三世纪的《孔子算经》。其中有一题云：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何”？书中给出的解法是：“术曰：三三数之剩二，置一百四十；五五数之剩三，以二百一十减之即得”。接着给出了一般解法：凡三三数剩一，则置十五；一百六以上，以一百五减之即得。孙子问题，在中国民间流传很广，有“秦王暗点兵”、“韩信点兵”、“剪管术”、“隔墙算”等名称。宋人周密（1232－1298年）《志雅堂杂抄》称“鬼谷算”，对“物不知数”的解法中三个乘数作诗引出：
“三岁孩儿七十稀，五留廿一事尤奇。
七度上元（15）重相会，寒食清明便可知”。
明代程大位《算法统宗》的诗歌，更为明显：
“三人同行七十稀，五树梅花廿一枝；七子团圆整半月，除百零五便得知。”
《孙子算经》给出了下面同余式组的解法：
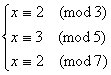
这里模数3、5、7是两两互质的，所以[3，5，7]=3×5×7=3×35=5×21=7×15且
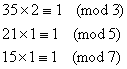
其解为：
推广到一般，设一次同余式组为：
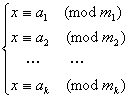（1）
式中
都是整数。如果
即两两互质。并设
且
，则组（1）的全部解为
也就是说一次同余式（1）的解化归为解K个同余式的问题：
秦九韶称mi称为定母，V为衍母，Mi为衍数.xi为乘率。也就是说，秦九韶的解法最后归结到解下面一种类型的同式问题。即A、B为互质的两整数，求出一整数
,使满足同余式
其中A为定母，B为衍数，求出的称乘率。秦九韶把求乘率的方法称“大衍求一术”。秦九韶先从B中屡减A，使其余数G<A,称G为寄数。大衍求一术说：“置寄右上，定居古下，天元一于左上。”先立一图式如下：
然后“先以右上除右下，所得商数与左上一相生，入左下，然后乃以后行上下，以少除多，递互除之，所得商数，随即递累乘，归左行上下，须使右上末后奇一而止，乃验左上所得，以为乘率”。举例如下：
算式如下：
得=5
一般来说，就是
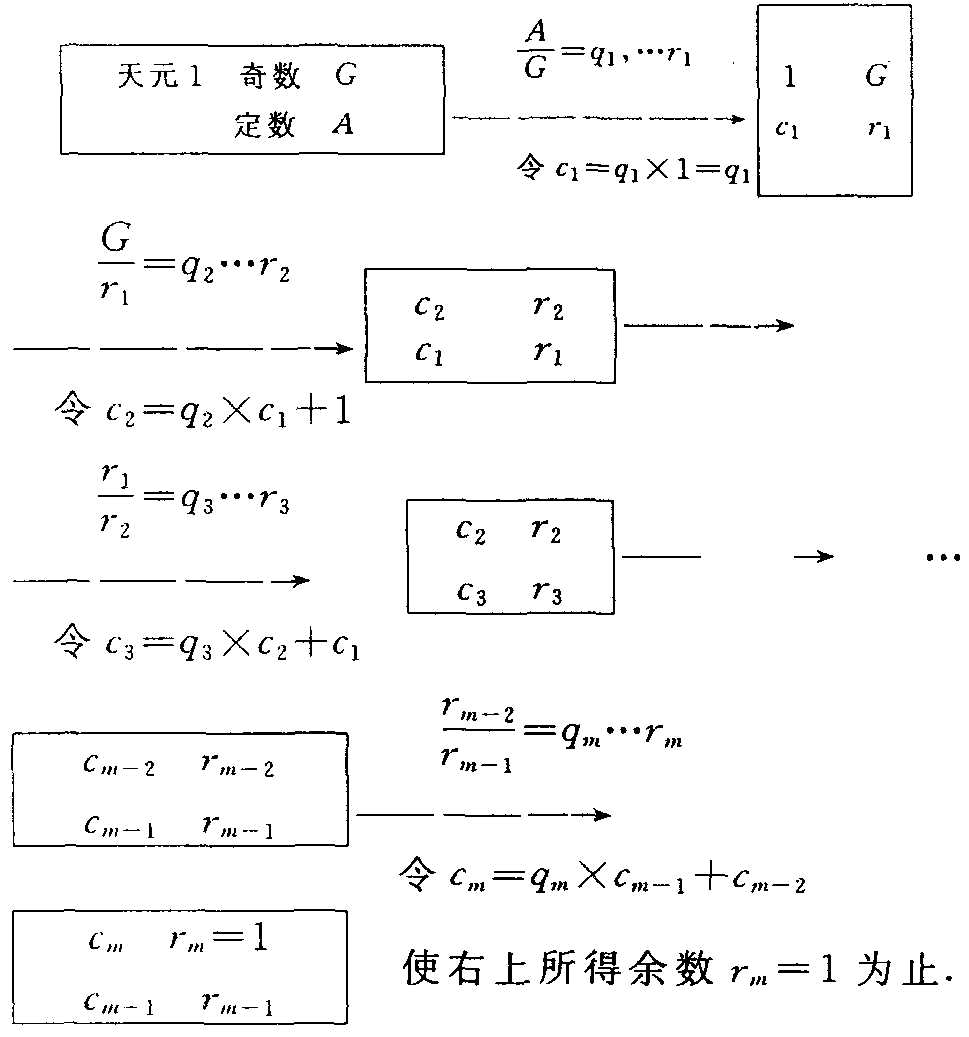
此时左上所得cm即为乘率，即=cm。
现在证明=cm。由上计算变换式的箭头线上下得两组等式：
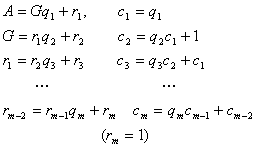
设
，则由上两组等式可以推出：
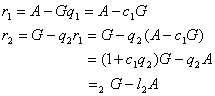
当rm=1时，最后一等式为
，由此可知：
再根据
得
.在各种计算问题中，所给的模数mi不一定两两互素，且不可能都是整数。秦九韶把模数分为四种。1.元数：指一般整数；2.收数：指小数；3.通数；指分数；4.复数：指皆为10”的倍数。秦九韶把后三种先化为第一种，然后把不互素的化为互素。大衍求一术在明中叶以后几乎失传，直到十九世纪才由一些数学家阐发出来，特别是黄宗宪的《求一术通解》（公元1874年）对mi不两两互素时，更有很好的解决办法。